Special Relay Circuit, PTO

Printed From: the12volt.com
Forum Name: Relays
Forum Discription: Relay Diagrams, SPDT Relays, SPST Relays, DPDT Relays, Latching Relays, etc.
URL: https://www.the12volt.com/installbay/forum_posts.asp?tid=144244
Printed Date: May 12, 2025 at 4:58 PM

Topic: Special Relay Circuit, PTO

Posted By: hmontgomery
Subject: Special Relay Circuit, PTO
Date Posted: March 20, 2018 at 9:29 AM

Using TWO switches to energize the coil on a relay. When one switch is turned off and turned back on I do not want the coil to re-energize

Thank you for your support

-------------
specred

Replies:

Posted By: the12volt
Date Posted: March 20, 2018 at 10:55 AM

Is this being used in a vehicle with the key in the accessory or ignition position? Do you want both switches to have to be turned off then back on for the relay coil to re-energize? Please tell us exactly what it is you're trying to do.

-------------
posted_image

the12volt • Support the12volt.com

Posted By: hmontgomery
Date Posted: March 20, 2018 at 11:09 AM

Automotive application.
Switch on the Dash to Select PTO. (Positive to coil) Transmission to confirm neutral to allow PTO to operate.(Negative to coil) When vehicle is put into gear (no neutal signal) the PTO will disengage (preventing overspeed of PTO). When vehicle stops and is placed back into neutral PTO attempts to reconnect. I do not want the PTO to reconnect when transmission goes back to neutral.
Thanks for your support.

-------------
specred

Posted By: the12volt
Date Posted: March 20, 2018 at 12:35 PM

Let's see if I understand your description.
You have an on/off switch on the dash that switches 12V+.
You have a neutral switch that supplies ground when the transmission is in neutral.
You want the ground from the neutral switch to allow the coil of a relay to enegize only one time after the dash switch is turned on until the transmission is put into gear.
Is this correct?

-------------
posted_image

the12volt • Support the12volt.com

Posted By: hmontgomery
Date Posted: March 20, 2018 at 12:54 PM

That is correct

-------------
specred

Posted By: the12volt
Date Posted: March 20, 2018 at 2:24 PM

I'm on the road without my laptop, but have it figured out in my head. It will take three additional SPDT relays to control your relay as you described. If it's not too late when I get home, I'll draw it up for you this evening. If not, I'll post it tomorrow morning.

-------------
posted_image

the12volt • Support the12volt.com

Posted By: hmontgomery
Date Posted: March 20, 2018 at 2:42 PM

Thanks

-------------
specred

Posted By: the12volt
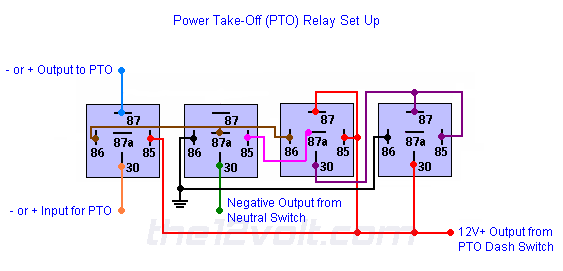
Date Posted: March 20, 2018 at 9:13 PM

The relay on the left is the relay you wanted to control. 30 on the first relay is your input. 87 on the first relay is your output to allow the PTO to operate. The second relay from the left allows the negative output from the neutral switch to pass to the coils of the first and third relays until it passes only once after the dash switch is turned on, energizing the coil of the first relay only once (and for as long as the transmission is in neutral), while the fourth relay creates a latch and opens the second relay through the normally closed contacts of the third relay (immediately after the transmission is put into gear) to prevent the output of the neutral switch from energizing the coil of the first relay (and third relay) again. When the dash switch is turned off or power is removed from the dash switch, the entire setup resets.

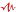posted_image

-------------
posted_image

the12volt • Support the12volt.com

Posted By: hmontgomery
Date Posted: March 21, 2018 at 6:34 AM

Thank you Will test in the near future and post results

-------------
specred